Profit vs Efficiency Maximization (transcript)

Pricing modes determine the conflicts between profit maximization and efficiency maximization.

Profit is maximized when marginal revenue (MR) from selling the product is equal to marginal cost (MC) of producing it.

Caption:

Profit maximization

MR = MC

Economic efficiency is maximized when price (P) from selling the product is equal to marginal cost (MC) of producing it.

Caption:

Efficiency maximization

P = MC

When price (P) is equal to marginal revenue (MR), both profit and efficiency are maximized.

Caption:

Max Profit = Max Efficiency

When P = MR = MC

Whether price is equal to marginal revenue or not depends on how pricing is done.

We will compare and contrast two modes of pricing, namely single pricing vs perfect price discrimination.

Caption:

Single pricing vs perfect price discrimination

TR

L

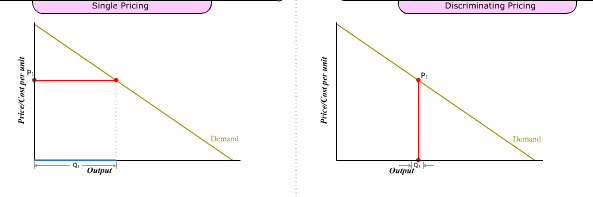
Single price (Psp) applies to all units sold.

Therefore Psp is an average price.

i.e., every buyer pays the same price even though some are willing to pay more.

R

Discriminating price (Pdp) applies only to the marginal unit sold.

Therefore Pdp price is a marginal price.

i.e., every unit is sold at a different highest possible price.

L

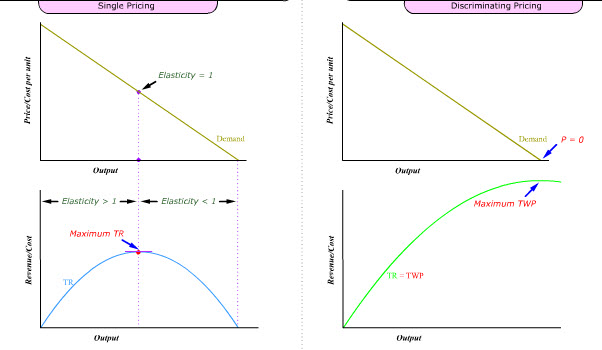
When a single-pricing firm faces a downward sloping demand curve, it must search for the maximum profit price. e.g., a firm in monopoly or monopolistic competition is such a price searcher

As the price searcher lowers its price, total revenue will first increase when sales increases faster than price decreases.

i.e., elasticity of demand > | 1 |

TR (total revenue) would reach a maximum when the sales increases no faster than price decreases.

i.e., elasticity of demand = | 1 |

Then TR decreases as sales increases slower than price decreases.

i.e., elasticity of demand < | 1 |

R

If the firm can sell each unit of output according to the buyer's willingness to pay (i.e., reservation price), the total revenue generated will be much larger and reaches its maximum when price charged is equal to zero.

This total revenue generated through perfect price discrimination can be called total willingness to pay (TWP)

L

Observation #1: Because single price is an average price, single-pricing seller's TR is affected by the elasticity of demand. TR maxs out when elasticity = 1.

R

Observation #2: Because discriminating price is a marginal price, price-discriminating seller's TR (i.e., TWP) maxs out only when price = 0.

MR

L

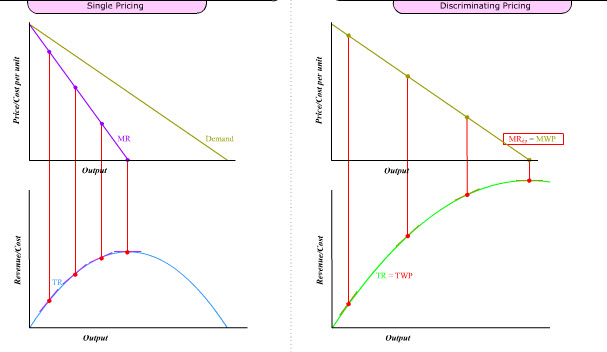
From the single-pricer's TR curve, we can derive the marginal revenue (MRsp) at any output level from the slope of TR.

R

From the discriminating pricer's TR curve (TWP), we can derive the marginal revenue (MRdp) at any output level from the slope of TWP.

Observation #1: MRdp is the same as the marginal willingness to pay (MWP).

L

Observation #2: TR reaches its maximum when MRsp = 0. This happens mid-point down the straight-line demand curve.

R

Observation #3: TWP reaches its maximum when MRdp = 0. This happens at the end of the demand (=MWP) curve.

L

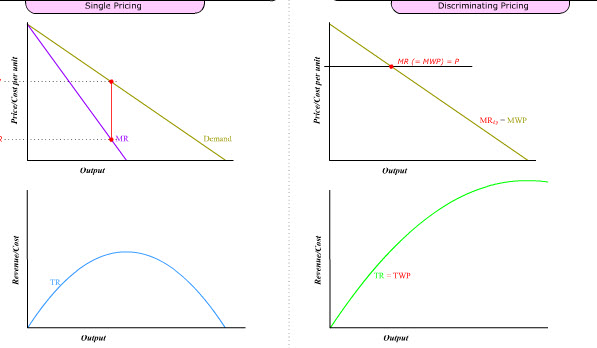
Observation #4: Under single pricing, MR < P because price must be lowered for all units in order to sell one more unit.

R

Observation #5: Under discriminating pricing, MR (= MWP) = P because each unit is sold at a different price.

Profit

Regardless of how pricing is done, profit is maximized when marginal revenue (MR) from selling the product is equal to marginal cost (MC) of producing it.

Caption:

Profit maximization

MR = MC

L

Under single pricing, profit is maximized where MRsp = MC.

R

Under discriminating pricing, profit is maximized where MRdp = MC.

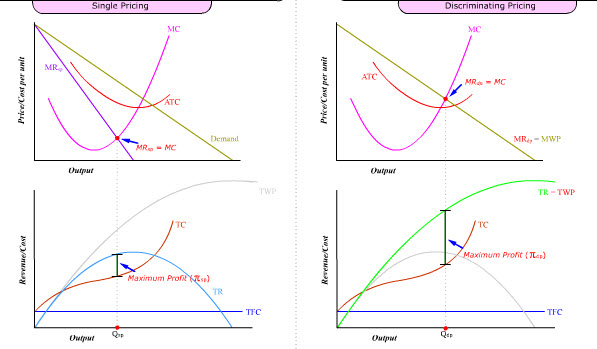
Although the same rule to maximize profit is followed under single pricing and perfect price discrimination, the resulting output level and profit level are quite different:

Observation #1: Qdp > Qsp.

πdp > πsp.

L

Observation #2: If the single-price searcher tries to produce at Qsp2 (= Qdp) where Psp = MC, total profit would be lower.

Efficiency

This difference in profit and output levels between single pricing and perfect price discrimination is a direct result of the different total revenue curves faced by the two types of sellers.

L

Under single pricing, economic profit is measured by (TR - TC) at any given output level.

For example, at maximum profit output (Qsp), where MR = MC, economic profit = πsp.

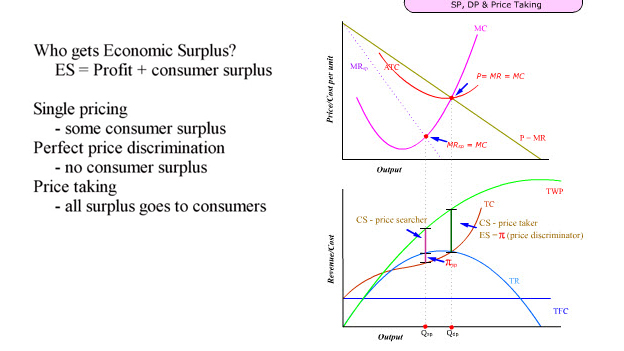
Since buyers are not being charged their reservation price for every unit they buy, there is a gap between what they are willing to pay (TWP) and what they actually pay (TR). This gap (TWP - TR) is known as consumer surplus.

The sum of profit (TR-TC) and consumer surplus (TWP-TR) is equal to economic surplus (TWP-TC).

Caption:

Economic surplus = TWP - TC

Economic surplus = consumer surplus + profit

ESsp = CSsp + πsp.

----

Economic surplus is maximized when P = MC.

When economic surplus is maximized, economic efficiency is by definition maximized because marginal benefit (indicated by P) from consuming it is equal to the additional cost (MC) of producing it..

Caption:

Efficiency maximization

P = MC

But if the single-price searcher tries to produce where Psp = MC, total profit would be lower.

Observation #1: Under single pricing, higher consumer surplus can be obtained only at the expense of economic profit after the maximum profit output level is reached.

R

Under discriminating pricing, economic profit is measured by (TWP - TC) at any given output level.

For example, at maximum profit output (Qdp), where MR = MC, economic profit = πdp.

---

But, (TWP - TC) also measures the economic surplus. Since Pdp = MC at Qdp, economic surplus (ESdp) is also maximized.

When ESdp = πdp, consumer surplus = 0.

Observation #2: Under discriminating pricing, maximizing economic surplus will also maximize profit.

Observation #3: But under discriminating pricing, higher economic profit (and higher output) is achieved at the expense of consumer surplus compared with single pricing.

Observation #4: If the only condition for simultaneously maximizing profit and economic surplus is P = MR when MR = MC, price takers who must accept the market price as given also satisfy the condition of P = MR at the firm level. But unlimited entry will lead to zero profit (TR = TC). So the economic surplus generated by P = MC goes entirely to consumers.

Caption:

Single pricing - some consumer surplus

Perfect price discrimination - no consumer surplus

Price taking - all surplus goes to consumers

Loss

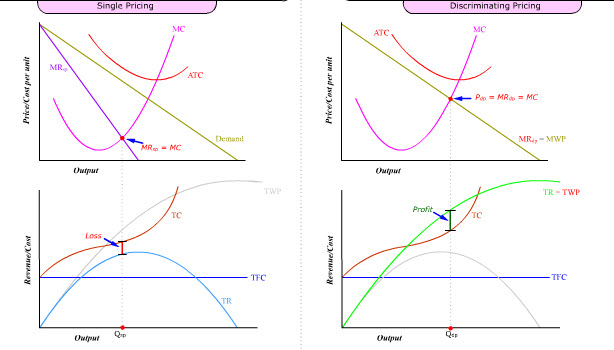
Perfect price discrimination not only produces higher profit and higher efficiency. It may also be able to stay in business after it is no longer profitable for the single pricer.

L

When the fixed cost is high, TC could be entirely above TR. The single-pricing firm suffers economic loss even when MRsp = MC.

R

But as long as TC is below TWP, the price-discriminating firm still enjoys economic profit when MRdp = MC.

L

Observation #1: Since a money-losing firm would go out of business, it cannot generate consumer surplus even though TWP-TC is still positive at the money-losing output level.

R

Observation #2: Although a price-discriminating firm captures the entire consumer surplus, its product still offers utility to customers at different affordable prices.